Funciones cuadráticas.
Definición: Una función cuadrática \(y=f(x)\) es una función de la forma, $$ y=ax^2+bx+c$$ donde \(a,~~b,~~c~~~\in~~\mathbb{R}~~\land~~a\neq0\) (si \(a=0\) la función es lineal).
Si \(b=0\) la función se transforma en \(y=ax^2+c\), si \(c=0\) se transforma en \(y=ax^2+bx,\) además la forma conónica de \(y=ax^2+bx+c\) es, $${(x-h)}^2=4p(y-k)$$ la cual puede escribirse en la forma estándar o normal para una función cuadrática como,
Forma estándar
$$y=a\left(x-h\right)^2+k$$
Gráficas de funciones cuadráticas.
A diferencia de las ecuaciones lineales la gráfica de una ecuación o función cuadrática es una curva llamada parábola de extensión infinita. Estas serán analizadas analiticamente a profundidad al estudiar las secciones cónicas.
La manera más fácil de realizar una gráfica de cualquier función matemática es utilizar un programa de graficación que sea capaz de mostrar con claridad los detalles de ésta, sin embargo, para la compresión y realización de un buen bosquejo a mano de la gráfica de una función cuadrática, se recomienda conocer un mínimo de cinco o seis puntos por donde pase la gráfica. Los puntos más convenientes para este fin son deducidos analíticamente como sigue: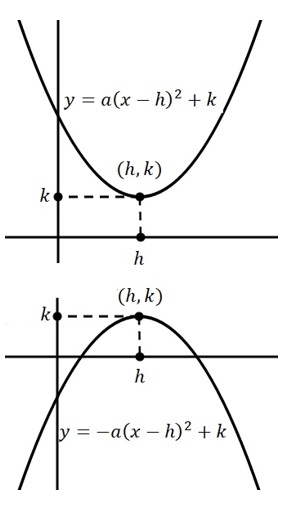
\(1.\) Vértice \((h,k)\) de la parábola,
$$\left(h,k\right)=\left(-\frac{b}{2a},f\left(-\frac{b}{2a}\right)\right)$$
\(2.\) Intersecciones en eje de abscisas (eje \(x\)), son los puntos para los cuales \(ax^2+bx+c=0\) para \( \mathbb{R}\). Si \(ax^2+bx+c=0\) no tiene solución en \(\mathbb{R},\) no hay intersección con el eje \(x.\)
\(3.\) Intersección en eje de ordenadas (eje \(y\)), hacer \(x=0\) en \(y=ax^2+bx+c\) de donde se tiene el punto \(\left(0,c\right),\) por ser \(y=c\) la intersección.
\(4.\) Determinar las coordenadas de dos o más puntos evaluando la expresión cuadrática \(y=ax^2+bx+c.\) Los valores más convenientes son \(x=h-n_1\) al junto de \(x=h+n_2\) (un valor a la izquierda y a la derecha).
\(5.\) Unir todos los puntos con una curva suave.
Como se podrá notar realizar un esbozo de una función cuadrática no conlleva un desafío mayor a la resolución de una ecuación cuadrática, para esto puede usar el método de su preferencia.
Valor máximo o mínimo de la parábola.
El valor máximo o mínimo de una función cuadrática siempre ocurre en el punto \(V\left(h,k\right)\) que es vértice, cuyas coordenadas para \(y=ax^2+bx+c\) como ya de ha dicho son
$$\left(h,k\right)=\left(-\frac{b}{2a},f\left(-\frac{b}{2a}\right)\right)$$
Si se tiene la forma estándar \(y=a(x-h)^2+k\) entonces ya se tiene el punto \((h,k)\) y en ambos casos,
1. Si \(a>0\) la parábola abre hacia arriba y \((h,k)\) es mínimo.
2. Si \(a< 0\) la parábola abre hacia abajo y \((h,k)\) es máximo.
Amplitud de la gráfica en una parábola.
Al escribir \(y=a{(x-h)}^2+k\) o como un trinomio \(y=ax^2+bx+c\) el valor \(a\) representa además del resultado ya conocidos (sentido de hacia dónde abre la curva), la amplitud de la parábola, y de esto se pueden realizar otras tres afirmaciones importantes más:
1. Cuanto más cerca esté el \(\left|a\right|\) de cero, la parábola es más abierta.
2. Cuanto más cerca de uno es el \(\left|a\right|\) la parábola es más cercana a la gráfica de \(y=x^2\) desplazada.
3. Cuanto más lejos de uno esté el \(\left|a\right|,\) la parábola es más cerrada, y ambas “ramas” se acercan más al eje de ordenada.
Intersecciones
Se denominan intersecciones a los puntos donde la gráfica de la función interseca (corta) uno de los ejes de coordenadas, estás pueden ser de dos tipos.
1. Intersecciones en eje de abscisas (eje\(x\)), puntos para los cuales \(ax^2+bx+c=0\) en \(\mathbb{R}.\) Si \(ax^2+bx+c=0\) no tiene solución en \(\mathbb{R}\) no hay intersección conel eje \(x\).
2. Intersección en eje de ordenadas eje \(y\)
Hacer \(x=0\) en la forma estándar o en el trinomio \(y=ax^2+bx+c\) , de donde se tiene el punto \((0,c)\).
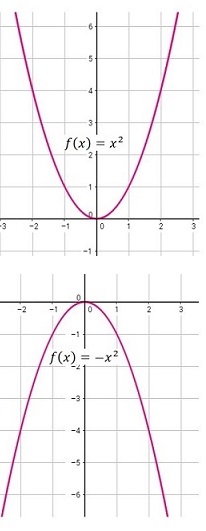Ejemplo 1. Realizar un esbozo de las gráficas de:
\(1.~~ f(x)=x^2\) y \(2.~~ f(x)=-x^2\)
Solución: comparando \(y=x^2\) con la función \(y=a\left(x-h\right)^2+k\) se tiene \(a=1\) (abre para arriba). \(h=0,~~~~k=0\) entonces el vértice es \(V=(0,0)\).
Para la función \(y=-x^2:~~ a=-1\) (abre para abajo) \(h=0,\ \ k=0\), entonces el vértice es \(V=(0,0)\). Realizando tablas se encuentran los puntos y las gráficas son como en la figura.
Estas gráficas son las formas más simple para la gráfica de una función cuadrática, partiendo de ellas se pueden realizar diversas transformaciones a la gráfica comomuestra la tabla de más abajo.
Transformaciones básicas a la gráfica de \(y=x^2\)
\begin{array}{l l} {\rm Gráfica}&{\rm Dezplazamiento}\\ y=x^2& {\rm Gráfica ~original.}\\ y=x^2+k & k ~{\rm unidades~ hacia~ arriba.}\\ y=x^2-k&k ~{\rm unidades ~hacia ~abajo.}\\ y=(x-h)^2& h~ {\rm unidades~ hacia~ la derecha.}\\ y=(x+h)^2&h ~{\rm unidades ~hacia~ la~ izquierda}\\ y=(x-h)^2+k& {\rm Dezplazaminto ~horizontal~ y ~vertical}\\ y=a(x-h)^2+k&{\rm Amplitud}~ a~ {\rm ~y ~desplazamiento~ horizontal~ y~ vertical.}\end{array}
Ejemplo 2. Realizar un bosquejo de la gráfica de la función \(y=x^2-x-6\).
Solución: para determinar el vértice, se escribe la forma estándar como sigue.
\begin{align}
&V=\left(h,k\right)=\left(-\frac{b}{2a},f\left(-\frac{b}{2a}\right)\right)\\
&V=\left(\frac{1}{2},f\left(\frac{1}{2}\right)\right)=\left(\frac{1}{2},-\ \frac{25}{4}\right)\end{align}
Intersección eje \(y\Longrightarrow y=c ~~\therefore~~ y=-6\).
Para la intersección en el eje \(x\) resolver \(x^2-x-6=0:\)
\(\left(x-3\right)\left(x+2\right)=0\Longleftrightarrow x_1=3~~~x_2=-2\)
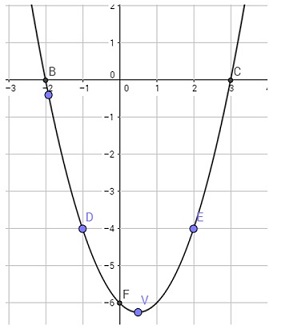Determinando algunos puntos:
como \(h=\frac{1}{2}\), por conveniencia se escogen los valores \(x=1/2-3/2=-1\) y \(x=1/2+3/2=2\) de donde resultan los puntos \(D\left(-1,-4\right)\) y \(E(2,-4)\) como se muestra en la tabla.
\begin{array}{c| c| c| c| c| c|}
x&-2&-1&0& 1/2& 2&3\\ \hline
y&0&-4&-6&-25/4&-4&0\end{array}
El esbozo de la gráfica de la función se muestra en la figura de la izquierda.
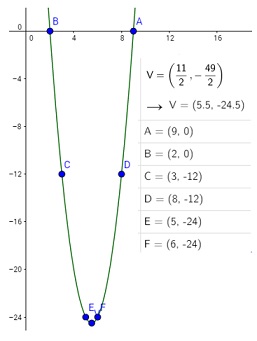
Ejemplo 3. Realizar un bosquejo de la gráfica de la función \(f(x)=2x^2-22x+36.\)
Solución: del ejercicio uno (ver los ejercicios) se tienen el vértice \(V\left(h,k\right)=\left(\frac{11}{2},\frac{49}{2}\right)\); la intersecciones con el eje de ordenadas \((0,36)\) y en el eje de abscisas \((9,0)\) y \((2,0).\). Para determinar un punto a la iquierda de \(h=\frac{11}{2}\) y otro a la derecha, se elige \(x=3\) y \(x=8\) de donde \(f(3)=f(-8)=-12\). Note que \(f(5)=f(6)=-24\) es un valor muy cercacno a \(k=\frac{49}{2}\) esta es la razón por la que se eligió \(x=3\) y \(x=8\).
Para más contenidos y luego clic en la pestaña del contenido deseado.
tab-2
Para más contenidos y luego clic en la pestaña del contenido deseado.tab-15
Para más contenidos y luego clic en la pestaña del contenido deseado.Forma estándar. Dada la función \(f(x)=2x^2-22x+36\)
\(a.\) Escribir la ecuación estándar de la función cuadrática.
\(b.\) Escribir las coordenadas del vértice determinando si es un máximo o mínimo de \(f(x).\)
\(c.\) Determinar las intersecciones con los ejes si los hay.
Número de unidades a producir. El ingreso por cierto artículo en un proceso industrial está dado por la expresión \(I\left(u\right)=-0.41u^2+1640u+2\ 000\) donde \(u\) son las unidades producidas del artículo. Determine el número de unidades que se deben producir para maximizar el ingreso y cuál es el ingreso máximo.
Altura máxima. Para un cuerpo que se mueve con aceleración constante, su ecuación de posición como función del tiempo, está dada por la expresión \(S=\frac{1}{2}at^2+v_0t+s_0\) donde \(S\) es la posición, \(a\) es la aceleración, \(t\) es el tiempo, \(v_0\) es la velocidad inicial y \(s_0\) es la posición inicial. Si se lanza verticalmente una bala de cañón desde el suelo con una velocidad inicial de \(50ft/s\).
\(a.\) ¿Determine la máxima altura que alcanza?
\(b.\) Estime el tiempo aproximado para que esto suceda.
Comparando formas. Dadas las funciones \(f(x)=2\left(x-5\right)^2+8\) y \({\rm g}\left(x\right)=-12\left(x+3\right)^2-4\) determinar los valores máximos (o mínimos) de las funciones y las coordenadas del vértice.
Trabajando con decimales. En cierta compañia los ingresos recibido por dos artículos está dados por las expresiones, $$\textcolor{#ff0080}{1}.~~f\left(x\right)=-0.5x^2+16x+5 \ \ \ \ \textcolor{#ff0080}{2}.~~{\rm g}\left(x\right)=0.003x^2+1.5x+12$$ Determine el valor máximo o mínimo de las funciones de ingreso.
Ingreso máximo. Para cierto producto de una compañía se ha determinado que el ingreso generado por su venta está dado por la expresión \(I\left(u\right)=-0.32u^2+512u+1500\) donde \(u\) es la cantidad de unidades vendidas del producto. Determine la cantidad de unidades que se deben fabricar para alcanzar el ingreso máximo y cuál es este ingreso.